Las cónicas

Cuando un cono circular recto es seccionado por un plano que no pasa por el vértice se pueden generar las siguientes curvas:
Elipse (e): el plano de corte no es paralelo a ninguna generatriz y corta a todas las generatrices del cono. Es una curva cerrada sin puntos en el infinito.
Parábola (p): el plano de corte es paralelo a una generatriz y tiene un punto en el infinito.
Hipérbola (h): el plano de corte es paralelo a 2 generatrices y tiene dos puntos en el infinito.
Circunferencia: el plano es ortogonal al eje de revolución y es un caso particular de la elipse en el que los dos ejes son iguales.
























Cónicas por homología:

http://homologias.blogspot.com.es/2010/10/construccion-de-conicas-por-homologia.html


Generación proyectiva de las cónicas.

Como en toda homología, todas las series de puntos se corresponden con otras series y los haces de rectas se corresponden con otros haces de rectas, una cónica se convierte en otra cónica por homología.
En la figura vemos varias propiedades de las homologías sobre las cónicas, los puntos homólogos S S’están alineados con el centro de proyección O, la rectas homólogas a a’ se cortan en el eje, los puntos del eje son dobles u homólogos de sí mismos, que quiere decir que si una figura corta al deje de homología en los puntos, su homóloga pasa por esos dos puntos, resultando estos invariables.
Las tangentes a una cónica lo son también a su homóloga. En dos crónicas homólogos el polo y polar de una tiene en sus homólogos otro polo y polar de la otra.
Cualquier cónica es posible transformarla en una circunferencia, de esta forma obtenemos puntos homólogos de la circunferencia obteniendo así nuevos puntos de la cónica.


Dados dos conjuntos de puntos SAB EDC sobre una cónica, si unimos cada uno de ellos con los del otro conjunto, excepto el que tiene en frente, tenemos en la intersección de todas las líneas tres puntos M N O que están alineados.
Como ya hemos visto este procedimiento sirve para obtener nuevos puntos de la cónica, que definida por cinco puntos obtenemos el sexto, el séptimo, etcétera.
Como en geometría los puntos y las rectas son términos correlativos, se pueden intercambiar unos por otros, de esta manera una cónica definida por cinco puntos se puede transformar en otra definida por cinco rectas. Cualquiera de estos cinco elementos se puede transformar resultando que podemos construir la cónica con cinco elementos cualesquiera entre puntos y rectas.


Dadas cuatro rectas abcd y un punto M incidente en una de ellas d determinar la cónica que pasando por el punto es tangente a las rectas dadas. Hacemos una circunferencia con un diámetro cualquiera (en color amarillo) tangente al punto incidente M sobre la recta d que va a ser el eje. Tomando una de las rectas d como eje de homología, la homóloga de la primera recta c será la recta tangente a la circunferencia desde la intersección del eje d con la recta c. La intersección de cada recta c y su homóloga c’ con la otra recta b y su homóloga b’ adyacentes respectivamente, determina una nueva recta que forma parte de una radiación (rectas en color verde) en cuyo vértice O está el centro de homología.
Si queremos obtener nuevos puntos de la elipse, tomamos dos puntos homólogos cualesquiera, por ejemplo R R’. Haciendo una recta cualquiera que pase por R’ vemos que corta a la circunferencia en P’, tenemos que alineando el centro de homología con P’ hasta que corte al eje sobre el punto V, y alineando V con R tenemos en la intersección con OP’ un punto de la elipse P.


Otro ejemplo análogo al anterior pero con el eje exterior a la cónica. Tenemos varios puntos sobre la cónica ABCE y una recta tangente m sobre un punto de ella A.
Haciendo una circunferencia amarilla tangente a la recta dada m y que pasa por el punto A, y alineando el centro de la homología A con los puntos de la elipse BCE, tenemos en la intersección con la circunferencia sus homólogos B’C’E’. Haciendo una recta cualquiera que pase por 2 puntos de la circunferencia C’ D’ corta al eje en un punto L, que unido con el punto homólogo conocido de la elipse C tenemos en la intersección de esta recta CL con la recta doble AD’ un nuevo punto de la elipse D.



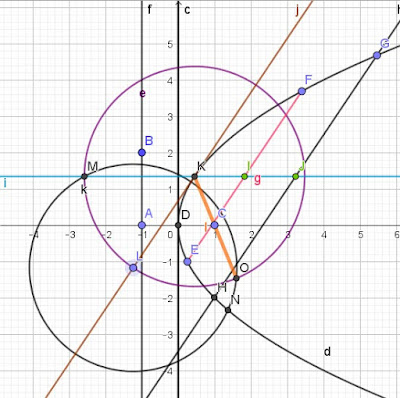
Correlativo del ejercicio anterior, tenemos como datos cuatro puntos y uno de ellos incidente sobre una recta tangente a la cónica. Se trata de determinar la cónica que pasa por los puntos BCDE y es tangente a la recta a en el punto B. Si tomamos el punto B como centro de homología y hacemos una circunferencia (en color amarillo) tangente a la recta a en este punto B, construimos las rectas dobles (rectas que pasan por el centro de homología B y por los puntos dados) que pasan por los puntos CDE. Éstas rectas cortan a la circunferencia en los puntos C’D’E’, respectivamente.
Las rectas homólogas CE C’E’se cortan en un punto del eje Y, otro par de rectas CD C’D’ se cortan en otro punto del eje S, dos puntos del eje YS determinan su posición.
Si queremos construir las tangentes a la cónica desde un punto cualquiera T, hacemos la tangente f desde ese punto a la circunferencia. Alineamos el punto de tangencia S’ con el centro de homología B hasta que corte al eje en un punto. Calculamos el homólogo de este punto y obtenemos el punto de tangencia S con la cónica y la tangente f u homóloga de la tangente f’ a la circunferencia.


En los casos anteriores los elementos, fueran puntos o fueran rectas tangentes, eran siempre incidentes (cuando existía una tangente, había un punto de la cónica que estaba sobre ella) y por lo tanto existía una única cónica que pasaba por los puntos y era tangente a las rectas. En el caso de que los elementos no sean incidentes, la solución ya no es sólo una única cónica sino que pueden ser más, por ejemplo, si tenemos tres puntos y dos tangentes a la cónica, como es el enunciado de este dibujo, el ejercicio tiene cuatro soluciones.
En el ejercicio sin embargo aparece resuelta una única solución, aquella en la que la circunferencia amarilla es tangente a las dos rectas dadas y pasa por dos puntos de la cónica.
Si alineamos el punto E el centro de homología O corta a la circunferencia en el punto E’. En este punto lo alineamos con otro punto T’ de la circunferencia y corta al eje en un punto que unido con E determina T en la intersección de la recta OT’. T es un punto de la cónica y si unimos su homólogo T’ con el punto de tangencia G’ tenemos un punto de intersección en el eje que unido al punto T tenemos en la prolongación el punto G en la intersección con la tangente b.

La parábola

La parábola es el lugar geométrico de los puntos que equidistan de otro llamado foco F y de una recta d llamada directriz. Análogamente es el lugar geométrico de los centros de las circunferencias tangentes a d e incidentes en el foco.
En toda parábola el vértice V equidista del foco y de la directriz: dV=VF, siendo la directriz una recta perpendicular al eje de la curva, que es su eje de simetría.
Para trazarla se hacen distintas perpendiculares al eje (por ejemplo la recta a), se toma la distancia de la perpendicular a la directriz da, y con ese radio se hace una circunferencia de centro en F y radio da. Los 2 puntos de intersección de da y a son puntos simétricos de la curva.











Podemos observar un ejemplo con números: por un punto cualquiera, el 5 por ejemplo, hacemos una perpendicular al eje. Con la distancia 5H (del punto 5 a la directriz D) hacemos centro en F y donde corte a la perpendicular que pasa por el punto 5 son los 2 puntos de la parábola.












2 rectas que se cortan se enumeran en orden creciente y decreciente en el mismo número de puntos. Se unen a continuación los puntos: 1 con 1, 2 con 2, etc., La curva resultante es la envolvente de la parábola tangente a las 2 rectas originales.













Se dividen 2 rectas horizontal y vertical en igual número de puntos como en la figura.
Sobre los puntos de la vertical se trazan horizontales y sobre los puntos de la horizontal se hacen rectas hacia el vértice de la parábola. La intersección de las 2 radiaciones son los puntos de la parábola.












2 rectas que se cortan se dividen en igual número de puntos en el orden de la figura, por ejemplo del 0 al 9. El punto 0 de una recta se une con los de la otra recta, y el punto 9 de la otra con todos los puntos de la otra recta. La intersección de las 2 radiaciones son los puntos de una parábola.











En rectas y circunferencias equidistantes, la intersección de cada recta con cada circunferencia son los puntos de curvas parabólicas.























Si en dos ejes a b cuya intersección es P dividimos en a segmentos iguales (1, 2, 3, 4,...)a partir de P y por un punto aleatorio M de a (a la derecha de a, como en el dibujo) hacemos circunferencias que pasen por 1, 2, 3, 4, y por M obtenemos circunferencias que cortan a la recta b en D, V, etc. Por la intersección de estas circunferencias y b hacemos horizontales que cortan a las verticales por 1 2 3 4 en puntos de la parábola.













Todas las parábolas tienen la misma forma, en el dibujo observamos parábolas iguales pero a distintas distancias. Si cogemos una de ellas y la escalamos siempre sale igual de forma a la anterior ya que todas son proporcionales. Son por tanto en esto las parábolas curvas iguales a las circunferencias, ya que también son siempre iguales de forma aunque puedan tener distintos tamaños.












http://teoremas-de-geometria.blogspot.com.es/2012/03/teorema-de-lambert.html


Dados el foco de la parábola y dos puntos de la misma AB, determinar el eje, el vértice y la directriz de la parábola.
Hacemos el arco capaz de 90° por AF, esto es, hacemos una circunferencia cuyo diámetro sea el foco F y un punto A.
Hacemos otra circunferencia que pase por el foco F y por el otro punto B.
Construimos una recta tangente -en color rojo- a las dos circunferencias y por el foco hacemos la perpendicular a esa tangente obteniendo de esta forma en su intersección el vértice V de la parábola. La línea que pasa por el vértice y el foco es el eje de la misma, para obtener la directriz hacemos centro en el vértice y tomando como radio la distancia del vértice V al foco F, hacemos un arco que corte al eje a esa distancia VF. En ese punto de intersección hacemos una perpendicular al eje -en verde- y esa es la directriz de la parábola. La resolución del ejercicio se basa en que toda tangente a la parábola intercepta a la recta roja que pasa por el vértice, en un punto que, unido al foco, se tiene que es perpendicular a la tangente.

La hipérbola

La hipérbola es el lugar geométrico de los puntos cuya diferencia de distancias a otros 2 fijos (llamados focos F1, F2) es constante e igual al eje mayor V1, V2.
En el dibujo se puede observar que la distancia de F2 a un punto (en azul) menos la distancia de F1 a ese punto (en verde) es igual a V1-V2.
Para construirla se cogen puntos (desde F1 hasta el infinito y del infinito hasta F2), por ejemplo desde A hasta V1 y se hace con ella un arco con centro en F1. A continuación se coge la distancia de A a V2 y se hace un arco con centro en F2. La intersección de los 2 arcos es un punto de la hipérbola.
















Se puede dibujar una rama hipérbólica por sección de un cono en sistema diédrico: el plano vertical a que corta al cono de vértice V determina la rama de la hipérbola. Para calcularla pasamos un plano vertical m por el eje del cono, éste corta a la circunferencia base del cono en P1, punto que proyectamos al alzado obteniendo P2 sobre la línea de tierra. El plano m corta en T al plano a, por este punto hacemos una vertical hasta que corte a P2-V en G. Los demás puntos se determinan de igual forma. Para determinar el vértice E se hace una circunferencia de centro O tangente al plano a, ésta corta a la línea de tierra en Z. Por Z se hace una vertical hasta que corta a la generatriz del contorno del cono en H y por este punto una horizontal que corta a V-O en E.














La intersección de un conjunto de circunferencias concéntricas equidistantes son curvas hiperbólicas.












Dados 2 vértices cualesquiera de una hipérbola AB, construimos un cuadrado con vértice en A y dividimos sus lados en partes iguales como se dispone en la figura. Desde B trazamos una radiación que pase por los puntos 1, 2, 3. Por los puntos del otro lado del cuadrado hacemos otra radiación hasta A.
La intersección de las dos radiaciones son los puntos de la curva.















Los puntos que se deben coger para construir la hipérbola deben estar, al igual que la elipse, entre los dos focos. La diferencia estriba en que en la elipse los puntos están dentro del segmento comprendido entre ambos puntos, mientras que en la hipérbola los puntos escogidos van desde un foco hacia el infinito y desde el infinito hacia el otro foco.
Manteniendo que toda recta tiene un punto en el infinito, se podría deducir que la hipérbola, al igual que la parábola tiene un único punto en el infinito, ya que pertenece a la misma curva y está localizado en la misma recta, no obstante en homología tenemos que cuando la recta límite corta la circunferencia en dos puntos, su figura homóloga ha de tener esos dos puntos en el infinito.












Para calcular las asíntotas o rectas tangentes a la hipérbola en el infinito hacemos una circunferencia c de centro O y radio O-F1. Por la intersección de las verticales por V1-V2 y la circunferencia c tenemos 4 puntos que unidos a O definen las asíntotas de la hipérbola.











Un ejemplo numérico lo tenemos con la hipérbola del dibujo: De V1 a un punto mide 28,69, con centro en F2 se hace un arco con esa medida.
De V2 a ese punto es 13,6, con centro en F1 se hace otro arco con esa medida que en la intersección con el arco anterior tenemos un punto de la hipérbola. La diferencia entre las 2 magnitudes es la distancia entre vértices: 15,09, según el concepto métrico de la hipérbola.

La elipse

La elipse es el lugar geométrico de los puntos cuya suma de las distancias de cada punto a 2 puntos fijos, llamados focos, es igual al eje mayor AB.
Dados los ejes AB y CD, hacemos centro en C con la medida del semieje mayor AO un arco que corta a AB en dos puntos, éstos son los focos: F y F’.
Tomamos puntos entre los focos a diferentes distancias, por ejemplo el punto 2, con la distancia 2A y centro en F hacemos un arco y con la distancia de B a F y centro en F’ hacemos otro arco. La intersección de los dos arcos son dos puntos de la elipse simétricos respecto a AB. Otros dos se pueden obtener por simetría respecto al eje CD.

















En sistema diédrico se puede calcular la elipse como sección del cono:
A la izquierda el plano rosa secciona al cono determinando así el eje mayor, cogemos una generatriz m que corta en la base en el punto E. Esta generatriz toca al plano de corte según vemos en el alzado en J2, bajamos este punto a la planta y obtenemos J1. La vertical por J1 hasta que corta a m1 determina Y1 que es un punto de la elipse. En el alzado abatimos la elipse para observar su verdadera forma.
A la derecha obtenemos los ejes, el plano de corte AB determina en el alzado el eje mayor. Por el punto medio de A2-B2 y por el vértice V2 pasamos la recta m. La recta m corta a la base del cono en L2, obtenemos la proyección en planta de este punto (L1) y lo unimos con V1, donde esta recta corta a la vertical por T1 obtenemos H. El eje menor de la elipse es TH.
En el alzado abatimos este eje para ver la verdadera forma de la elipse.















Según el teorema de Pascal, si cogemos seis puntos sobre una cónica, y los unimos dos a dos de la forma que muestra el dibujo del borde superior izquierdo-en amarillo-, tenemos en la intersección de esas radiaciones tres nuevos puntos XYZ que están siempre alineados.
Este teorema nos sirve para construir nuevos puntos de la cónica y nos demuestra que cinco elementos de la misma la definen. Estos elementos pueden ser puntos y/o rectas, indistintamente.
Dados los cinco puntos de la cónica ABDMN, determinar nuevos puntos de la misma.
1-Por el punto B se traza una recta cualquiera h, que corta a la recta que pasa por los puntos DN en un punto P.
2- Ese punto P lo unimos con el punto L, que es la intersección de las rectas que pasan por los puntos AN y BM. Tenemos de esta forma la recta que pasa por los puntos LP.
3- La recta que pasa por los puntos PL intercepta a la que pasa por los puntos MD en el punto S. la recta AS corta a la recta h en el punto Q, que es la solución. Otros puntos se calculan de forma análoga.















En toda elipse tenemos una circunferencia que es tangente a los vértices del eje mayor de la misma, se llama circunferencia principal -de color roja en la ilustración. Si hacemos centro en el vértice superior de un punto cualquiera del eje menor de la elipse con el radio de la circunferencia principal, obtenemos los focos F1 F2 en la intersección con el eje mayor de la elipse -a esta circunferencia la llamamos en el dibujo CP.
Circunferencia focal es aquella que tiene por centro uno de los focos de la elipse-por ejemplo el foco F2- y por radio la distancia entre los vértices del eje mayor de la elipse.
La elipse es el lugar geométrico de los centros de las circunferencias -a, b, c, d - que son tangentes a la circunferencia focal CF y que al mismo tiempo pasan por uno de los focos F1. Así tenemos que las circunferencias b (amarilla) a (verde) c tienen sus centros en puntos de la elipse, son tangentes a la circunferencia focal y uno de sus puntos pasa por el foco de la elipse F1. De esto se desprende como caso particular que la circunferencia d que determina los focos de la elipse y tiene su centro en un vértice del eje menor de ella, es tangente a la circunferencia focal.















La circunferencia principal de una elipse es el lugar geométrico de los puntos de intersección que determinan las perpendiculares trazadas desde los focos a las tangentes de la elipse. Esto quiere decir que se pueden trazar infinitos rectángulos tangentes a la elipse en dos de sus lados opuestos y cuyos otros lados pasen siempre por los focos de manera que los vértices de estos rectángulos pasen siempre por la circunferencia principal, que es aquella cuyo diámetro coincide con el diámetro mayor de la elipse.














En el dibujo observamos los rectángulos tangentes a la elipse cuyos lados pasan por los focos y cuyos vértices inciden en la circunferencia principal.














Una elipse la podemos construir por un método de afinidad, se trazan distintos diámetros por el centro de la elipse y en la intersección de las dos circunferencias de diámetros menor y mayor de la elipse trazamos líneas horizontales y verticales, respectivamente. La intersección de estas líneas son puntos de la elipse.














Aquí podemos observar un ejemplo numérico para la construcción de la elipse: el diámetro mayor de la elipse se ha separado en dos dimensiones: 20,84 y 43,65. Haciendo centro en los focos y con radio esas dos dimensiones tenemos un punto de la elipse.















Si hacemos las tangentes a una elipse podemos observar que estas son el eje de simetría de una curva que pasa por uno de los focos y otra curva que es un arco de la circunferencia focal -la forma de color rosa y la amarilla son simétricas y su eje de simetría es la línea de contacto entre ellas que es tangente a la elipse. Esta es otra forma de construir la elipse, si nos dan la circunferencia focal c y tomamos su centro F1 como uno de los focos de la elipse, basta con doblar el papel de forma que hagamos coincidir un punto de la circunferencia c con el otro foco F2. La línea por la que hemos doblado el papel es una tangente a la elipse ya que es el eje de simetría de la curva que al doblar el papel se ha solapado con el foco F2.













Construcción por haces proyectivos
Se dibuja un cuadrilátero paralelogramo y se dividen sus lados en partes equidistantes como en la figura. La intersección de haces que salen del punto medio de los lados superior e inferior hacia las divisiones equidistantes de la figura son los puntos de la curva.
Como el procedimiento se basa en un método de geometría proyectiva es válido para cualquier proyección.















Por ser un método proyectivo se conserva por proyección, no obstante es acosejable utilizar la proyección cilíndrica ya que hay que dividir los segmentos en partes iguales y ello resulta laborioso en una proyección cónica.
















Si en un cuadrilátero en el que se va a inscribir la elipse dividimos sus lados verticales en partes iguales, por ejemplo seis, y unimos el punto uno con el C, y hacemos lo mismo con el eje mayor de la elipse, lo dividimos en seis partes iguales y unimos el punto D con esos puntos como se muestra en la figura. La intersección de la recta que pasa por el punto D y el punto uno del eje mayor de la elipse con la recta que pasa por el punto c y el punto uno del segmento vertical tangente a la elipse por el punto B, es un punto M de la elipse.















Dado el diámetro a de una elipse determinar el otro diámetro conjugado. Se hace una recta paralela b al segmento dado y el punto medio M se une con el centro del diámetro dado O, que es el centro de la elipse. El segmento OM determina el diámetro conjugado de la elipse.
Si proyectamos los dos diámetros a c sobre una circunferencia-en la parte superior a’ c’-podemos observar que los dos diámetros transformados de los anteriores son perpendiculares entre sí.















Para construir una elipse por otro método de afinidad, basta con hacer triángulos semejantes cuyos vértices incidan por los puntos del eje menor de la elipse o por el diámetro de la circunferencia, ya que son coincidentes.
Dada la circunferencia que se va a transformar en la elipse y su diámetro a, dado un punto cualquiera de la elipse Z homólogo del centro de la circunferencia O, determinar la elipse afín de esta circunferencia.
Unimos el punto P con el punto Z y tenemos el triángulo rojo OPZ. Por un punto cualquiera u del diámetro a de la circunferencia hacemos otro triángulo semejante -en color verde-, esto quiere decir que por él punto U hacemos una recta m’ paralela a la recta m. Hacemos otra recta UT paralela a la recta OP hasta que corte la circunferencia en el punto T. Por el punto T hacemos una paralela d’ a la recta d hasta que corte a la recta m’, la intersección de las dos rectas m’ d’ nos determina el punto Z’, que es un punto de la elipse.
Para hallar nuevos puntos de la elipse basta con hacer triángulos semejantes al anterior, esto es, triángulos que tengan sus lados paralelos y cuyos vértices pasen por la recta a y por puntos de la circunferencia.

















Dados los ejes conjugados de la elipse (los correspondientes por proyección a los ejes ortogonales de la circunferencia), determinar el eje mayor y menor de la elipse.

Método de Mannheim:
Dados los ejes conjugados de la elipse (en azul claro w, q), hacemos centro en O (intersección de los ejes conjugados) con la distancia OB (B es el extremo del semieje conjugado) y dibujamos el arco a.
Creamos una línea rosa t perpendicular a OB y donde esta corta al arco a obtenemos Z, lo unimos con N (extremo del otro diámetro conjugado). Hacemos centro en V, punto medio del segmento ZN y hacemos una circunferencia de radio VZ.
Unimos V con O obteniendo como intersección con la circunferencia de centro V el punto P: PN (m) es la dirección del eje mayor de la elipse y su perpendicular m’ la dirección del otro eje.
La longitud de los dos ejes es: OP para el eje menor y OF (F es la intersección de m´ con OP) para el eje mayor. Los ejes los determinamos gráficamente como la intersección de C (circunferencia verde) con k (eje paralelo a m’) y de C´ (circunferencia roja) con ñ (eje paralelo a m).















Teorema de Dandelin

Existen 1 o 2 esferas tangentes interiores a un cono y a un plano de sección. Este plano determina los focos de las cónicas en los puntos de tangencia con las esferas.
Los planos que definen la intersección de las esferas con el cono (2 circunferencias) y el plano de la cónica determina las directrices de la misma.















En este perfil observamos 2 esferas (en rosa y amarillo) con un plano p tangente a ambas. Este plano p que secciona al cono según la elipse azul m de eje mayor TY (extremos de la sección del cono). La intersección de p y los planos donde las esferas son tangentes al cono: j, k, son 2 rectas paralelas al eje menor.
El plano p lo proyectamos y abatimos para obtener en verdadera forma la elipse. El eje mayor TY de la elipse se transforma al proyectarla en T’Y’, el centro de la elipse es el punto medio O’ por ser una curva simétrica respecto a los dos ejes principales. Los focos son los puntos de tangencia DF de las esferas con el plano p proyectados sobre la elipse: D’F’. Para obtener el semieje menor de la elipse LO se hace un plano e por O perpendicular al eje del cono en cuya sección abatida lo observamos en verdadera magnitud. A continuación lo colocamos sobre la elipse azul ortogonal a T’Y’ y a partir del centro de la elipse: L’O’.















El caso de la parábola.

Observamos en el dibujo una esfera tangente a la sección parabólica del cono en el foco de la parábola. El eje de la parábola e pasa por el punto de tangencia de la esfera con el plano de sección y corta al plano donde el cono y la esfera son tangentes, esto es, el plano que pasa por la recta M.
Los dos planos -el que secciona el cono y el de contacto entre la esfera y el cono- pasan por las dos rectas e m, respectivamente, y se cortan en una recta d y que es la directriz de la parábola.
El teorema de Dandelin nos determina con facilidad el foco de una sección del cono. La solución a los ejercicios para la determinación de los focos de las cónicas consiste en hacer una esfera tangente a la sección y al cono y el punto de contacto de la esfera con la sección cónica es un foco de la cónica.















En este dibujo observamos en un perfil el cono separado en dos trozos por un corte, con la esfera tangente al plano de sección en el punto a.
Observamos también que el plano m -azul- que es el plano que pasa por donde el cono y la esfera son tangentes, corta al plano de sección del cono en la recta d, que es la directriz que la parábola.














Tangentes a las cónicas.
Para hacer las tangentes t1 t2 a una cónica cualquiera desde un punto P, se trazan dos secantes s1 s2 a la misma y en los cuatro puntos de intersección con la cónica se hacen las diagonales n, m y las secantes d, a. La intersección de nm y da son dos puntos por donde pasa la polar. La polar corta a la cónica en los puntos de tangencia desde donde podemos trazar las tangentes t1 t2 desde P.










Con la construcción de una cadena de Steiner se puede construir una cónica:

http://inversas-de-figuras.blogspot.com.es/2012/02/circunferencia.html

http://tangentes-a-la-parabola.blogspot.com/ http://tangentes-a-la-hiperbola.blogspot.com/ http://tangentes-a-la-elipse.blogspot.com/ http://polaridad-involucion.blogspot.com/ Polo C y polar (recta verde). This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com Aplicaciones prácticas de las curvas cónicas y su existencia en la naturaleza. La parábola se da en los faros de los coches, en los focos, en las antenas de radio y televisión, en los radiotelescopios; todos ellos se sirven de la parábola cuyos rayos de proyección salen o entran paralelos al eje de la parábola desde o en dirección al foco. Se da también en los arcos de los puentes, en el diseño de las cabezas de misiles, en cables de puentes colgantes con carga de distribución uniforme, en estufas eléctricas, en telescopios reflectantes, en un fluido de un recipiente rotatorio por efecto de la fuerza centrífuga, excepcionalmente en órbitas planetarias bisagras entre elipses e hipérbolas -entre lento y rápido desplazamiento, respectivamente-, en superficies de carrocerías y fuselajes por su carácter aerodinámico, en la trayectoria de la curva que describe un objeto al ser lanzado con campo gravitatorio homogéneo y despreciando la resistencia al aire, como por ejemplo un misil. La parábola no hay que equivocarla con la curva catenaria, de forma parecida, que es la curva que adopta una cuerda colgada desde dos de sus puntos por su peso. Cuando varios proyectiles se disparan desde un cañón en distintas direcciones, el conjunto de las trayectorias que siguen estos proyectiles definen una envolvente que nunca es rebasada por ninguna de las trayectorias. Esta envolvente es una parábola de revolución llamada de seguridad, (esto es la superficie generada por la revolución de una semiparábola). Esta envolvente de todas las parábolas tiene en su tangente por el vértice una línea que es directriz de todas las parábolas, esto es, una recta perpendicular a todos los ejes de las parábolas. La elipse se da en las órbitas de los cuerpos celestes que giran en torno a otro, en misiles con trayectoria intercontinental en los cuales hay mayor fuerza y donde g ya no es constante. La elipse se da en secciones de bóvedas y formas de distintos arcos, también en la perspectiva de nuestra percepción las circunferencias las podemos ver como elipses. La bóveda del techo del andén del metro tiene una curvatura elíptica, lo que facilita una buena acústica. Las piedras erosionadas por el agua del río son formas aproximadas a elipsoides cuyas secciones se acercan en la forma a secciones elípticas. La perspectiva oblicua de una circunferencia desde una proyección paralela o cilíndrica sobre un plano es una elipse (siempre y cuando los planos no sean paralelos), si la proyección es cónica resulta una cónica cualquiera. Si 2 jugadores nos pasamos el balón dentro de un recinto sin necesidad de tener que coger nunca la pelota, debemos disponer de un recinto con forma elíptica. Nos colocamos en los focos de la elipse y cuando el balón rebote con los muros en forma de elipse siempre irá a la otra posición donde está la otra persona, en el otro foco de la elipse. Si juego yo solo al frontón contra las paredes y quiero que el balón siempre venga de vuelta, la elipse debe tener sus 2 diámetros iguales, esto es, ser una circunferencia. La hipérbola se da en el redondeo de piezas, en la proyección de las sombras de casi todos los focos y pantallas que hay en la casa, en la intersección de las circunferencias equidistantes que provocan dos piedras lanzadas al agua, en las centrales térmicas de torres de refrigeración. La hipérbola es la curva fronteriza o envolvente de una zona de audio: un avión que se desplaza con velocidad constante y movimiento rectilíneo propaga el ruido de su motor en esferas crecientes. Según se desplaza las esferas que va dejando atrás son cada vez mayores y la curva envolvente de esas esferas es un paraboloide. La proyección ortogonal de estas esferas y del paraboloide es, respectivamente, un conjunto de círculos y una hipérbola envolvente a las mismas. Cuando un palo está clavado ortogonalmente sobre el suelo y es iluminado por el sol, la sombra que produce el extremo del palo es una hipérbola. Las curvas cónicas se dan en general en casi todos los diseños en los que se quiere que las superficies sean suaves y aerodinámicas, esto es, que no se note la transición entre en el enlace de las superficies, como son las superficies de cascos de barcos, de fuselajes de aviones, de carrocerías de automóviles, etcétera. http://la-aerodinamica.blogspot.com/ También se dan de forma genérica en los movimientos de cuerpos celestes, que según la fuerza de atracción puede generar cualquiera de las cónicas: si el objeto sigue una trayectoria rectilínea por el espacio -despreciando la curvatura del espacio- y es atraído por la órbita de otro describe una forma hiperbólica, excepcionalmente parabólica. Si el objeto que lo atrae tiene fuerza suficiente para incorporarlo en su propia órbita, éste describe una curva elíptica en cuyo foco está el objeto. Las bóvedas tienen por sección formas cónicas y los arcos suelen tener por lo general forma parabólica, elíptica o circular. Igual que en las leyes de la mecánica, que provocan que la trayectoria del balón salga de un foco de la elipse y choque con una pared del campo elíptico y vaya al otro foco, pasa lo mismo con las leyes de la reflexión y refracción en óptica con todas las cónicas. Un rayo de luz que salga de un foco rebota en la pared de un espejo elíptico y vuelve al otro foco. En el caso de la parábola si el punto de luz está en el foco de la misma, el rayo, al tocar la superficie parabólica, sale reflejado en una dirección paralela al eje de revolución del paraboloide por eso todos los faros son paraboloides de revolución, mientras que si la superficie es hiperbólica, el rayo de luz que sale del foco rebota con la superficie y sigue una dirección definida por ese punto y el otro foco.