En el dibujo se puede observar que la distancia de F2 a un punto (en azul) menos la distancia de F1 a ese punto (en verde) es igual a V1-V2.
Para construirla se cogen puntos (desde F1 hasta el infinito y del infinito hasta F2), por ejemplo desde A hasta V1 y se hace con ella un arco con centro en F1. A continuación se coge la distancia de A a V2 y se hace un arco con centro en F2. La intersección de los 2 arcos es un punto de la hipérbola.

-----------------------------------------------------------------------
Se puede dibujar una rama hipérbólica por sección de un cono en sistema diédrico: el plano vertical a que corta al cono de vértice V determina la rama de la hipérbola. Para calcularla pasamos un plano vertical m por el eje del cono, éste corta a la circunferencia base del cono en P1, punto que proyectamos al alzado obteniendo P2 sobre la línea de tierra. El plano m corta en T al plano a, por este punto hacemos una vertical hasta que corte a P2-V en G. Los demás puntos se determinan de igual forma. Para determinar el vértice E se hace una circunferencia de centro O tangente al plano a, ésta corta a la línea de tierra en Z. Por Z se hace una vertical hasta que corta a la generatriz del contorno del cono en H y por este punto una horizontal que corta a V-O en E.

------------------------------------------------------------------
La intersección de un conjunto de circunferencias concéntricas equidistantes son curvas hiperbólicas.

Pensemos en un lago en el que tiramos dos piedras, son los focos. Dividimos la distancia entre ellos en 3 partes para marcar un momento en el que las circunferencias pasan por esos puntos. Las circunferencias concéntricas se cortan en varios puntos que determinan una curva hipérbola.
Como las curvas crecen y se amplían cada vez más no pueden ser curvas cerradas como la circunferencia o la elipse, el carácter de curvas que se abren cada vez más, que van hacia el infinito, las convierte en en una curva asintótica que no puede ser otra que una cónica hipérbola, ya que la economía de la naturaleza genera las curvas más suaves entre los puntos y esta es una característica propia de las cónicas.
El centro de la hipérbola quedará entre los dos focos, hacemos centro en este punto con el radio hasta uno de los focos y obtenemos en las verticales por los vértices B C las intersecciones por donde pasan las dos asíntotas, además de por el centro B1.
Si unimos los puntos de intersección de las circunferencias concéntricas obtenemos las dos ramas hiperbólicas que pasan por ejemplo por los puntos B C del eje horizontal.
------------------------------------------------------------------
Dados 2 vértices cualesquiera de una hipérbola AB, construimos un rectángulo con vértice en A y dividimos sus lados en partes iguales como se dispone en la figura. Desde B trazamos una radiación que pase por los puntos 1, 2, 3 en disposición vertical. Por los puntos del otro lado del cuadrado hacemos otra radiación hasta A.
La intersección de las dos radiaciones son los puntos de la curva.

------------------------------------------------------------------
Los puntos que se deben coger para construir la hipérbola deben estar, al igual que la elipse, entre los dos focos. La diferencia estriba en que en la elipse los puntos están dentro del segmento comprendido entre ambos puntos, mientras que en la hipérbola los puntos escogidos van desde un foco hacia el infinito y desde el infinito hacia el otro foco.
Manteniendo que toda recta tiene un punto en el infinito, se podría deducir que la hipérbola, al igual que la parábola tiene un único punto en el infinito, ya que pertenece a la misma curva y está localizado en la misma recta, no obstante en homología tenemos que cuando la recta límite corta la circunferencia en dos puntos, su figura homóloga ha de tener esos dos puntos en el infinito.

--------------------------------------------------------------------
En la figura podemos ver en planta y alzado a la izquierda (Sistema diédrico) y en color negro un hipérboloide de revolución, se engendra por una rama hiperbólica que gira en torno a un eje. (También se puede engendrar mediante líneas rectas, por lo que es una superficie reglada alabeada). El contorno de la superficie en el alzado es una hipérbola con sus dos ramas correspondientes.
Para construir el dibujo basta con hacer un cilindro determinado por sus generatrices, si giramos una de las dos circunferencias la de la base o la de la cara superior permaneciendo quieta la otra, tenemos que las generatrices del cilindro aparecen oblicuas, ya no son rectas ortogonales a la base y por tanto la superficie tiene una concavidad en la zona central, tal y como se ve en el alzado. Para que se entienda mejor la figura se han puesto distintas proyecciones de la misma en color azul a la derecha y en el centro la superficie de color rojo gira en torno a un eje de revolución de color verde.
------------------------------------------------------------------
Para calcular las asíntotas o rectas tangentes a la hipérbola en el infinito hacemos una circunferencia c de centro O y radio O-F1. Por la intersección de las verticales por V1-V2 y la circunferencia c tenemos 4 puntos que unidos a O definen las asíntotas de la hipérbola.

------------------------------------------------------------------
Un ejemplo numérico lo tenemos con la hipérbola del dibujo: De V1 a un punto mide 28,69, con centro en F2 se hace un arco con esa medida.
De V2 a ese punto es 13,6, con centro en F1 se hace otro arco con esa medida que en la intersección con el arco anterior tenemos un punto de la hipérbola. La diferencia entre las 2 magnitudes es la distancia entre vértices: 15,09, según el concepto métrico de la hipérbola.

------------------------------------------------------------------
Intersección de recta e hipérbola
Para calcular la intersección de una recta HL (en color negro) con una hipérbola se construye la circunferencia focal que es aquella que tiene como centro uno de los focos E de la hipérbola y por radio la distancia entre los dos vértices BD de la misma.
Se calcula el simétrico F’ del otro foco F respecto a la recta dada, dibujamos una circunferencia que pase por el foco y su simétrico y que al mismo tiempo corte a la circunferencia focal en dos puntos MN. La intersección de la línea definida por MN y de la línea definida por el foco y su simétrico F-F’ determina el centro radical CR.
Si construimos las tangentes a la circunferencia focal desde el centro radical CR obtenemos dos puntos de tangencia OP que unidos con el otro foco C determinan en la prolongación e intersección con la recta dada los puntos de corte T1 T2 de esta recta con la hipérbola.
------------------------------------------------------------
------------------------------------------------------------
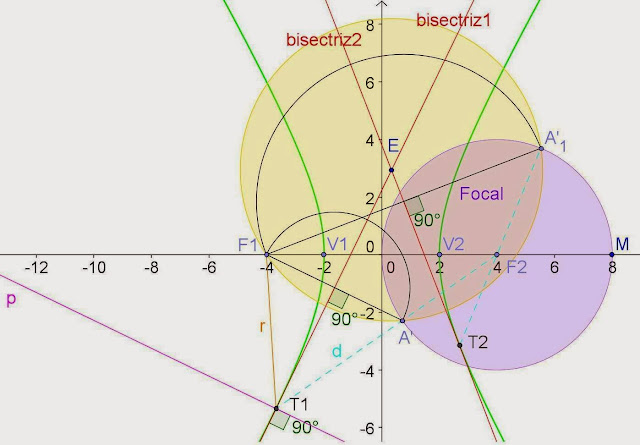
Tangentes a la hipérbola.
Para
construir las rectas tangentes desde un punto E a la hipérbola, construimos una
circunferencia (en color amarillo) cuyo centro sea el punto dado y el radio sea
la distancia desde ese punto hasta uno de los focos E-F1.
A continuación construimos la circunferencia
focal (en color violeta), que es aquella que tiene centro en el otro foco F2 y como radio la distancia entre los vértices de la
hipérbola V1-V2.
Podemos
observar en el dibujo que las dos circunferencias se cortan en dos puntos
A’-A’1, si alineamos estos puntos con el segundo foco F2, obtenemos al
prolongar estas dos rectas dos puntos de intersección con la hipérbola T1 y T2,
estos dos puntos son los de tangencia de las rectas tangentes a la hipérbola
desde el punto exterior dado E. En consecuencia unimos estos puntos de
tangencia con el punto dado y
construimos las dos rectas rojas que son en realidad las dos tangentes a la
curva.
Como podemos
observar en el dibujo le hemos denominado a cada una de ellas bisectriz, 1 y 2
respectivamente. Ello es debido a que si tomamos uno de los puntos de tangencia,
por ejemplo T1, y lo unimos con los dos focos mediante dos rectas, podemos
observar que ambas tienen por bisectriz la recta tangente, en este primer caso
la bisectriz1.
Además se cumple que respecto a esta bisectriz
o tangente desde un punto, que el primer foco F1 tiene como punto simétrico
respecto a la primera bisectriz el punto de intersección entre las dos
circunferencias A’, igualmente el otro punto de intersección de las dos
circunferencias A’1 es el simétrico de
este primer foco F1 respecto a la segunda bisectriz.
La recta
perpendicular p a la curva que pasa por los puntos de tangencia –en este caso
por T1- es en realidad la perpendicular a la tangente en ese punto, como
podemos observar en el dibujo.
------------------------------------------------------------------
En el dibujo podemos observar un punto M desde el que se han trazado las dos tangentes -en color verde- a la hipérbola, para construir las tangentes por M hemos hecho una circunferencia de color marrón que pasa por uno de los focos H de la hipérbola. A continuación hemos dibujado la circunferencia focal CF con centro en el otro foco K y hemos alineado este foco con los puntos de intersección H' H'1 de las dos circunferencias obteniendo en la prolongación de estas rectas los puntos de intersección con la hipérbola, esto dos puntos N O son los puntos de tangencia de las rectas tangentes desde el punto M.
Como podemos observar en el dibujo, los puntos de intersección de las dos circunferencias tienen por simétricos respecto a las rectas tangentes el otro foco H. Como novedad respecto al ejercicio anterior podemos observar que la circunferencia principal, que es aquella que tiene como centro L el de la hipérbola y radio desde el centro de la hipérbola hasta uno de los vértices J de la hipérbola, intercepta en las tangentes o ejes de simetría los puntos medios de los simétricos anteriores: H y H'1, son dos puntos diametralmente opuestos respecto al centro Q.
Asimismo H y H', son dos puntos diametralmente opuestos respecto al centro P.
-------------------------------------------------------
Tenemos una rama hiperbólica JK de color verde a la derecha y queremos calcular el centro E
de esa hipérbola y la dirección de los ejes xy, trazamos dos cuerdas secantes - en color negro-
a la derecha y tomamos sus puntos medios MN por los que trazamos una recta naranja,
si volvemos a hacer la misma operación con otras dos cuerdas -No se repite en el dibujo-
obtenemos otra recta que determina en su intersección con la anterior el centro E de la hipérbola.
Por ese centro hacemos una circunferencia de radio aleatorio que corta las ramas hiperbólicas
según 4 puntos, los lados del rectángulo que definen estos 4 puntos determina la dirección de
ambos ejes.
de esa hipérbola y la dirección de los ejes xy, trazamos dos cuerdas secantes - en color negro-
a la derecha y tomamos sus puntos medios MN por los que trazamos una recta naranja,
si volvemos a hacer la misma operación con otras dos cuerdas -No se repite en el dibujo-
obtenemos otra recta que determina en su intersección con la anterior el centro E de la hipérbola.
Por ese centro hacemos una circunferencia de radio aleatorio que corta las ramas hiperbólicas
según 4 puntos, los lados del rectángulo que definen estos 4 puntos determina la dirección de
ambos ejes.
-----------------------------------------------------------
Tenemos una rama hiperbólica de color
verde que pasa por los puntos KJ.
Se trata de calcular los ejes
principales, los focos, los vértices y las asíntotas.
Los ejes principales los calculamos por el
mismo método que la elipse, a continuación tomamos un punto H del eje
focal y hacemos una recta perpendicular I a EC, hasta que corta a la rama
hiperbólica en L.
Hacemos una
circunferencia de centro E con el radio EH, hacemos otra circunferencia con el radio EB.
Esta última circunferencia corta al eje vertical y en M, por donde hacemos una paralela MN
al eje focal, está línea paralela corta a la circunferencia anterior de radio EH en el punto N,
por el que trazamos una recta vertical que
corta a la línea horizontal por L en O.
La línea OE es la asíntota g de la curva, y su simétrica g’ respecto al eje y es la otra asíntota.
--------------------------------------------------------
Para dibujar una hipérbola- en color verde en el dibujo- podemos dibujar una elipse- de color negro- en cuyo foco B hacemos descansar circunferencias c de distinto tamaño, al hacer tangentes GD FC desde los dos vértices CD del eje mayor de la elipse a esa circunferencia c obtenemos puntos H que corresponden a una hipérbola.
Esta figura corresponde a la proyección de una elipse girada 90 grados en el espacio sobre la que se apoya una esfera c de diferentes tamaños en el foco B de la elipse y un cono tangente a esa esfera que tiene en el contorno los vértices CD del eje mayor de la elipse y que al variar su tamaño produce que los vértices de ese cono definan una hipérbola en el espacio.
Si dibujamos esferas que se apoyan en el vértice C de la elipse y desde los focos AB de la elipse hacemos dos tangentes - en color rojo- a esa esfera verde, tenemos que la intersección de las dos tangentes nos produce el punto K, todos los puntos intersección de esas tangentes corresponden a una elipse.
----------------------------------------------------
Demostración gráfica de definición métrica de la hipérbola
--------------------------------------------------------------
Dibujamos las circunferencias focales (focal1 y focal2) que son aquellas que tienen por centro el foco y el radio la distancia entre los dos vértices de la hipérbola.
Como podemos observar la focal1 corta a la circ. azul de radio G-foco2 en un punto C' que unido con el vértice 2 genera un segmento cuya mediatriz t2 es la tangente a la cónica. Para obtener el punto de tangencia TG1 basta con unir el punto de intersección C' con el foco1 y prolongar esa línea hasta que corte a la mediatriz t2 en el punto TG1.
Si hacemos lo mismo del otro lado, la intersección de la circunferencia focal2 con la otra circ. azul de radio G-foco1, unido con el foco1 determina un segmento cuya mediatriz es la otra tangente t1. Si unimos ese punto D' de intersección con el foco2 y prolongamos la línea hasta que corte a la mediatriz tendremos el otro punto de tangencia TG2.
Como podemos observar si desde los focos trazamos perpendiculares a las tangentes obtenemos puntos SUVK que quedan sobre la circunferencia principal que es aquella verde cuyo diámetro pasa por los vértices y el centro es el de la hipérbola.










Gracias, no encontraba en ningún sitio la explicación de cómo dibujar las asíntotas :)
ResponderEliminarGracias a ti. Saludos
Eliminar