En toda parábola el vértice V equidista del foco y de la directriz: dV=VF, siendo la directriz una recta perpendicular al eje de la curva, que es su eje de simetría.
Para trazarla se hacen distintas perpendiculares al eje (por ejemplo la recta a), se toma la distancia de la perpendicular a la directriz da, y con ese radio se hace una circunferencia de centro en F y radio da. Los 2 puntos de intersección de da y a son puntos simétricos de la curva.

---------------------------------------------------------------------------------
Podemos observar un ejemplo con números: por un punto cualquiera, el 5 por ejemplo, hacemos una perpendicular al eje. Con la distancia 5H (del punto 5 a la directriz D) hacemos centro en F y donde corte a la perpendicular que pasa por el punto 5 son los 2 puntos de la parábola.

---------------------------------------------------------------------------------
2 rectas que se cortan se enumeran en orden creciente y decreciente en el mismo número de puntos. Se unen a continuación los puntos: 1 con 1, 2 con 2, etc., La curva resultante es la envolvente de la parábola tangente a las 2 rectas originales.

Si cogemos los puntos medios de los segmentos que nos quedan en la intersección del conjunto de rectas definiremos una curva parabólica tangente a las dos rectas que la inscriben -Dibujo de la izquierda en color rojo.
Por contra si cogemos los puntos de intersección de el conjunto de líneas que se cortan obtendremos otra parábola que es secante a las dos rectas que inscriben al conjunto de todas las rectas- dibujo de la derecha en color verde.
---------------------------------------------------------------------------------
Se dividen 2 rectas horizontal y vertical en igual número de puntos como en la figura.
Sobre los puntos de la vertical se trazan horizontales y sobre los puntos de la horizontal se hacen rectas hacia el vértice de la parábola. La intersección de las 2 radiaciones son los puntos de la parábola.

---------------------------------------------------------------------------------
2 rectas que se cortan se dividen en igual número de puntos en el orden de la figura, por ejemplo del 0 al 9. El punto 0 de una recta se une con los de la otra recta, y el punto 9 de la otra con todos los puntos de la otra recta. La intersección de las 2 radiaciones son los puntos de una parábola, según refieren algunos libros.

Sin embargo, geogebra nos dice otra cosa, que la curva es una elipse:
---------------------------------------------------------------------------------
En rectas y circunferencias equidistantes, la intersección de cada recta con cada circunferencia son los puntos de curvas parabólicas.


---------------------------------------------------------------------------------
Construimos su perpendicular r por k y luego la recta simétrica de h respecto al eje de simetría r, obteniendo z.
Donde corte z al eje principal n tenemos el foco A.
La directriz c es la perpendicular al eje principal n por B, que es el simétrico del foco A respecto al vértice V.
---------------------------------------------------------------------------------
Si en dos ejes a b cuya intersección es P dividimos en a segmentos iguales (1, 2, 3, 4,...)a partir de P y por un punto aleatorio M de a (a la derecha de a, como en el dibujo) hacemos circunferencias que pasen por 1, 2, 3, 4, y por M obtenemos circunferencias que cortan a la recta b en D, V, etc. Por la intersección de estas circunferencias y b hacemos horizontales que cortan a las verticales por 1 2 3 4 en puntos de la parábola.

---------------------------------------------------------------------------------
Todas las parábolas tienen la misma forma, en el dibujo observamos parábolas iguales pero a distintas distancias. Si cogemos una de ellas y la escalamos siempre sale igual de forma a la anterior ya que todas son proporcionales. Son por tanto en esto las parábolas curvas iguales a las circunferencias, ya que también son siempre iguales de forma aunque puedan tener distintos tamaños.

http://teoremas-de-geometria.blogspot.com.es/2012/03/teorema-de-lambert.html
El hecho de que la parábola sea igual siempre en forma, aunque varíe su tamaño está relacionado con la circunferencia, curva en la que también se da el caso de que todas las circunferencias son iguales, también de forma aunque puedan ser de distinto tamaño.
La razón la podemos ver en el dibujo, la parábola es el lugar geométrico de los centros de las circunferencias tangentes a una recta directriz y que pasan por el foco de la parábola. Como según el concepto de la parábola la distancia del foco a un punto es igual que la distancia de ese punto a la recta directriz, tenemos que estos dos radios iguales determinan la circunferencia cuyo centro es un punto de la parábola. Si ampliamos la parábola o la reducimos, el dibujo de las circunferencias y la curva parabólica es siempre igual, ya que los dos radios considerados de cada circunferencia también son invariables, por tanto la curva tiene siempre la misma forma.
---------------------------------------------------------------------------------
Dados el foco de la parábola y dos puntos de la misma AB, determinar el eje, el vértice y la directriz de la parábola.
Hacemos el arco capaz de 90° por AF, esto es, hacemos una circunferencia cuyo diámetro sea el foco F y un punto A.
Hacemos otra circunferencia que pase por el foco F y por el otro punto B.
Construimos una recta tangente -en color rojo- a las dos circunferencias y por el foco hacemos la perpendicular a esa tangente obteniendo de esta forma en su intersección el vértice V de la parábola. La línea que pasa por el vértice y el foco es el eje de la misma, para obtener la directriz hacemos centro en el vértice y tomando como radio la distancia del vértice V al foco F, hacemos un arco que corte al eje a esa distancia VF. En ese punto de intersección hacemos una perpendicular al eje -en verde- y esa es la directriz de la parábola. La resolución del ejercicio se basa en que toda tangente a la parábola intercepta a la recta roja que pasa por el vértice, en un punto que, unido al foco, se tiene que es perpendicular a la tangente.

---------------------------------------------------------------------------------
Intersección de recta y parábola
---------------------------------------------------------------------------------
El caso de la parábola en el Teorema de Dandelin
Observamos en el dibujo una esfera tangente a la sección parabólica del cono en el foco de la parábola. El eje de la parábola e pasa por el punto de tangencia de la esfera con el plano de sección y corta al plano donde el cono y la esfera son tangentes, esto es, el plano que pasa por la recta M.
Los dos planos -el que secciona el cono y el de contacto entre la esfera y el cono- pasan por las dos rectas e m, respectivamente, y se cortan en una recta d y que es la directriz de la parábola.
El teorema de Dandelin nos determina con facilidad el foco de una sección del cono. La solución a los ejercicios para la determinación de los focos de las cónicas consiste en hacer una esfera tangente a la sección y al cono y el punto de contacto de la esfera con la sección cónica es un foco de la cónica.

En este dibujo observamos en un perfil el cono separado en dos trozos por un corte, con la esfera tangente al plano de sección en el punto a.
Observamos también que el plano m -azul- que es el plano que pasa por donde el cono y la esfera son tangentes, corta al plano de sección del cono en la recta d, que es la directriz que la parábola.

Demostración de que la parábola es una sección cónica:
---------------------------------------------------------------------------------
Nos dan de una parábola, el punto H el eje focal y el vértice de la misma, hay que obtener el foco. Podemos obtener puntos de la parábola al dividir el eje focal hasta el punto G en un número de partes iguales a la división que hacemos entre H y G.
el vértice de la parábola es el de la radiación de todas las líneas qué pasa por ese punto y por W U S etc, los cinco divisiones sobre el segmento horizontal superior
mientras que por el segmento HG tenemos cinco divisiones por las que hacemos 5 horizontales y cortan a las líneas anteriores en los puntos T R, por ejemplo, pudiendo obtener los demás puntos hasta llegar a los 5 o todos los que queramos.
Hacemos una secante RT que no sea vertical, ya que la vertical nos va a dar una línea que va a pasar por el vértice y no puede localizar el foco.
Cogemos entonces la secante RT, que corta la parábola en esos puntos
Cogemos el punto medio y hacemos una línea verde que sea paralela al eje focal DG, qué es el eje que pasa por el vértice.
Este eje corta a la parábola es un punto T, para obtener ese punto podemos seguir el procedimiento de los haces proyectivos donde una línea va desde el vértice hasta el punto U que es un quinto del segmento WH, esto intercepta a la línea verde n en el punto T que es el punto buscado
Por el punto T hacemos una línea paralela al segmento RT, tenemos entonces la tangente.
Por el punto T hacemos la perpendicular a la tangente y obtenemos la normal, que con la línea verde n forma un ángulo alfa.
Ese mismo ángulo lo debemos poner hacia abajo desde el punto T de manera que hacemos una línea que sale de T hasta que intercepta al eje focal en foco.
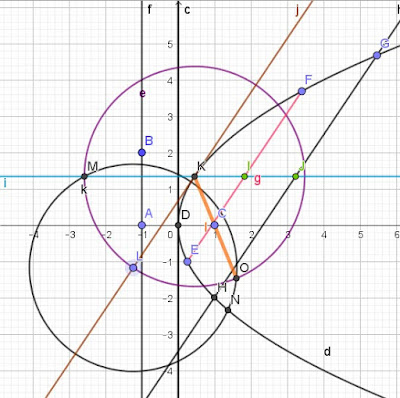
Trazamos dos cuerdas verdes g u, luego cogemos los puntos
medios P O por los que hacemos una recta gris azulada t. Esa dirección de la
recta es la dirección de la recta focal j, por tanto cogemos el punto medio O de
una de las cuerdas –u- y dibujamos una perpendicular –v- a la recta gris
azulada –t- de esta forma tenemos la perpendicular en color marrón –v- que corta
a la parábola s en dos puntos –N Ñ- tomamos el punto medio-H- del eje focal por
el que hacemos una recta verde oscura –j- paralela a la que es gris azulada –t-
y ya tenemos el eje focal de la parábola.
La línea gris azulada –t- corta a la parábola en un punto –R-
y tomamos en ese punto la tangente morada –m- que corta a una circunferencia azul
de cualquier radio en X, éste lo tomamos como centro de una circunferencia
naranja, con la distancia de radio XR. La intersección de las dos
circunferencias, azul y naranja, nos da un punto W que lo unimos con el punto R
y esta línea recta corta al eje focal en
un punto D que es el foco. La intersección C del eje focal con la parábola es
el vértice y la distancia entre el vértice y el foco la tomamos y la ponemos a
la izquierda del vértice obteniendo el punto A que es por donde pasa la
perpendicular al eje focal y la llamamos directriz.
El eje focal será la perpendicular por O a t.












Excelente aporte.
ResponderEliminarMuchas gracias. Siento no contestar antes, no vi el mensaje. Saludos.
Eliminar