La elipse

La elipse es el lugar geométrico de los puntos cuya suma de las distancias de cada punto a 2 puntos fijos, llamados focos, es igual al eje mayor AB.
Dados los ejes AB y CD, hacemos centro en C con la medida del semieje mayor AO un arco que corta a AB en dos puntos, éstos son los focos: F y F’.
Tomamos puntos entre los focos a diferentes distancias, por ejemplo el punto 2, con la distancia 2A y centro en F hacemos un arco y con la distancia de B a F y centro en F’ hacemos otro arco. La intersección de los dos arcos son dos puntos de la elipse simétricos respecto a AB. Otros dos se pueden obtener por simetría respecto al eje CD.


















----------------------------------------------------------------------


En sistema diédrico se puede calcular la elipse como sección del cono:
A la izquierda el plano rosa secciona al cono determinando así el eje mayor, cogemos una generatriz m que corta en la base en el punto E. Esta generatriz toca al plano de corte según vemos en el alzado en J2, bajamos este punto a la planta y obtenemos J1. La vertical por J1 hasta que corta a m1 determina Y1 que es un punto de la elipse. En el alzado abatimos la elipse para observar su verdadera forma.
A la derecha obtenemos los ejes, el plano de corte AB determina en el alzado el eje mayor. Por el punto medio de A2-B2 y por el vértice V2 pasamos la recta m. La recta m corta a la base del cono en L2, obtenemos la proyección en planta de este punto (L1) y lo unimos con V1, donde esta recta corta a la vertical por T1 obtenemos H. El eje menor de la elipse es TH.
En el alzado abatimos este eje para ver la verdadera forma de la elipse.




















----------------------------------------------------------------------


Según el teorema de Pascal, si cogemos seis puntos sobre una cónica, y los unimos dos a dos de la forma que muestra el dibujo del borde superior izquierdo-en amarillo-, tenemos en la intersección de esas radiaciones tres nuevos puntos XYZ que están siempre alineados.
Este teorema nos sirve para construir nuevos puntos de la cónica y nos demuestra que cinco elementos de la misma la definen. Estos elementos pueden ser puntos y/o rectas, indistintamente.
Dados los cinco puntos de la cónica ABDMN, determinar nuevos puntos de la misma.
1-Por el punto B se traza una recta cualquiera h, que corta a la recta que pasa por los puntos DN en un punto P.
2- Ese punto P lo unimos con el punto L, que es la intersección de las rectas que pasan por los puntos AN y BM. Tenemos de esta forma la recta que pasa por los puntos LP.
3- La recta que pasa por los puntos PL intercepta a la que pasa por los puntos MD en el punto S. la recta AS corta a la recta h en el punto Q, que es la solución. Otros puntos se calculan de forma análoga.

------------------------------------------------

En toda elipse tenemos una circunferencia que es tangente a los vértices del eje mayor de la misma, se llama circunferencia principal -de color roja en la ilustración. Si hacemos centro en el vértice superior de un punto cualquiera del eje menor de la elipse con el radio de la circunferencia principal, obtenemos los focos F1 F2 en la intersección con el eje mayor de la elipse -a esta circunferencia la llamamos en el dibujo CP.
Circunferencia focal es aquella que tiene por centro uno de los focos de la elipse-por ejemplo el foco F2- y por radio la distancia entre los vértices del eje mayor de la elipse.
La elipse es el lugar geométrico de los centros de las circunferencias -a, b, c, d - que son tangentes a la circunferencia focal CF y que al mismo tiempo pasan por uno de los focos F1. Así tenemos que las circunferencias b (amarilla) a (verde) c tienen sus centros en puntos de la elipse, son tangentes a la circunferencia focal y uno de sus puntos pasa por el foco de la elipse F1. De esto se desprende como caso particular que la circunferencia d que determina los focos de la elipse y tiene su centro en un vértice del eje menor de ella, es tangente a la circunferencia focal.


















---------------------------------------------------------------------------------

La circunferencia principal de una elipse es el lugar geométrico de los puntos de intersección que determinan las perpendiculares trazadas desde los focos a las tangentes de la elipse. Esto quiere decir que se pueden trazar infinitos rectángulos tangentes a la elipse en dos de sus lados opuestos y cuyos otros lados pasen siempre por los focos de manera que los vértices de estos rectángulos pasen siempre por la circunferencia principal, que es aquella cuyo diámetro coincide con el diámetro mayor de la elipse.































--------------------------------------------------------------------

En el dibujo observamos los rectángulos tangentes a la elipse cuyos lados pasan por los focos y cuyos vértices inciden en la circunferencia principal.
















---------------------------------------------------------------------------



Una elipse la podemos construir por un método de afinidad, se trazan distintos diámetros por el centro de la elipse y en la intersección de las dos circunferencias de diámetros menor y mayor de la elipse trazamos líneas horizontales y verticales, respectivamente. La intersección de estas líneas son puntos de la elipse.




















---------------------------------------------------------------------------






Aquí podemos observar un ejemplo numérico para la construcción de la elipse: el diámetro mayor de la elipse se ha separado en dos dimensiones: 20,84 y 43,65. Haciendo centro en los focos y con radio esas dos dimensiones tenemos un punto de la elipse.



















---------------------------------------------------------------------






Si hacemos las tangentes a una elipse podemos observar que estas son el eje de simetría de una curva que pasa por uno de los focos y otra curva que es un arco de la circunferencia focal -la forma de color rosa y la amarilla son simétricas y su eje de simetría es la línea de contacto entre ellas que es tangente a la elipse. Esta es otra forma de construir la elipse, si nos dan la circunferencia focal c y tomamos su centro F1 como uno de los focos de la elipse, basta con doblar el papel de forma que hagamos coincidir un punto de la circunferencia c con el otro foco F2. La línea por la que hemos doblado el papel es una tangente a la elipse ya que es el eje de simetría de la curva que al doblar el papel se ha solapado con el foco F2.
























---------------------------------------------------------


Construcción por haces proyectivos
Se dibuja un cuadrilátero paralelogramo y se dividen sus lados en partes equidistantes como en la figura. La intersección de haces que salen del punto medio de los lados superior e inferior hacia las divisiones equidistantes de la figura son los puntos de la curva.
Como el procedimiento se basa en un método de geometría proyectiva es válido para cualquier proyección.















Por ser un método proyectivo se conserva por proyección, no obstante es aconsejable utilizar la proyección cilíndrica ya que hay que dividir los segmentos en partes iguales y ello resulta laborioso en una proyección cónica.




















-------------------------------------------------------------------------------------




Si en un cuadrilátero en el que se va a inscribir la elipse dividimos sus lados verticales en partes iguales, por ejemplo seis, y unimos el punto uno con el C, y hacemos lo mismo con el eje mayor de la elipse, lo dividimos en seis partes iguales y unimos el punto D con esos puntos como se muestra en la figura. La intersección de la recta que pasa por el punto D y el punto uno del eje mayor de la elipse con la recta que pasa por el punto c y el punto uno del segmento vertical tangente a la elipse por el punto B, es un punto M de la elipse.




















-------------------------------------------------------------------------



Dado el diámetro a de una elipse determinar el otro diámetro conjugado. Se hace una recta paralela b al segmento dado y el punto medio M se une con el centro del diámetro dado O, que es el centro de la elipse. El segmento OM determina el diámetro conjugado de la elipse.
Si proyectamos los dos diámetros a c sobre una circunferencia-en la parte superior a’ c’-podemos observar que los dos diámetros transformados de los anteriores son perpendiculares entre sí.





















-----------------------------------------------------------

Las medianas de un  paralelogramo -líneas rojas- son los ejes conjugados de la elipse (transformados de  las rectas de color magenta ortogonales de la circunferencia afín -azul).
Construcción por pasos.

Si hacemos un cuadrilátero paralelogramo cualquiera inscrito en una elipse, al hacer las medianas, que son las rectas que pasan por los puntos medios de lados opuestos del cuadrilátero, obtenemos dos ejes de  la elipse, que son en realidad diámetros conjugados de la misma. Para comprobar que esto es cierto hacemos una circunferencia cualquiera que corte a la elipse, como por ejemplo la de color verde, y en los puntos de intersección con la elipse, OE, tomamos el punto medio Q y lo unimos con el centro de la elipse N. Al prolongar esta recta obtenemos en la intersección con la elipse  el extremo o vértice S. 

Si hacemos una circunferencia azul cuyo centro sea el de la elipse y radio el segmento anterior NS, estamos construyendo la circunferencia principal de la elipse -en color azul. 

Al proyectar los extremos de los diámetros rojos, esto es: MJHI mediante rectas perpendiculares al eje mayor de la elipse obtenemos en la intersección con la circunferencia azul los extremos correspondientes a los ejes reales de la circunferencia transformada de la elipse, aquella que correspondería por proyección a la curva anterior. Como podemos observar efectivamente los dos diámetros ortogonales de color magenta forman 90° y se transforman por proyección sobre la elipse en los diámetros rojos que corresponden a los conjugados de la misma.

Otro ejemplo:

las medianas -en amarillo- del paralelogramo inscrito en la elipse se transforman sobre la circunferencia en diámetros ortogonales -en naranja.

-------------------------------------------------------------------

Para construir una elipse por otro método de afinidad, basta con hacer triángulos semejantes cuyos vértices incidan por los puntos del eje menor de la elipse o por el diámetro de la circunferencia, ya que son coincidentes.
Dada la circunferencia que se va a transformar en la elipse y su diámetro a, dado un punto cualquiera de la elipse Z homólogo del centro de la circunferencia O, determinar la elipse afín de esta circunferencia.
Unimos el punto P con el punto Z y tenemos el triángulo rojo OPZ. Por un punto cualquiera u del diámetro a de la circunferencia hacemos otro triángulo semejante -en color verde-, esto quiere decir que por él punto U hacemos una recta m’ paralela a la recta m. Hacemos otra recta UT paralela a la recta OP hasta que corte la circunferencia en el punto T. Por el punto T hacemos una paralela d’ a la recta d hasta que corte a la recta m’, la intersección de las dos rectas m’ d’ nos determina el punto Z’, que es un punto de la elipse.
Para hallar nuevos puntos de la elipse basta con hacer triángulos semejantes al anterior, esto es, triángulos que tengan sus lados paralelos y cuyos vértices pasen por la recta a y por puntos de la circunferencia.



















-----------------------------------------------------------



Dados los ejes conjugados de la elipse (los correspondientes por proyección a los ejes ortogonales de la circunferencia), determinar el eje mayor y menor de la elipse.

Método de Mannheim:
Dados los ejes conjugados de la elipse (en azul claro w, q), hacemos centro en O (intersección de los ejes conjugados) con la distancia OB (B es el extremo del semieje conjugado) y dibujamos el arco a.
Creamos una línea rosa t perpendicular a OB y donde esta corta al arco a obtenemos Z, lo unimos con N (extremo del otro diámetro conjugado). Hacemos centro en V, punto medio del segmento ZN y hacemos una circunferencia de radio VZ.
Unimos V con O obteniendo como intersección con la circunferencia de centro V el punto P: PN (m) es la dirección del eje mayor de la elipse y su perpendicular m’ la dirección del otro eje.
La longitud de los dos ejes es: OP para el eje menor y OF (F es la intersección de m´ con OP) para el eje mayor. Los ejes los determinamos gráficamente como la intersección de C (circunferencia verde) con k (eje paralelo a m’) y de C´ (circunferencia roja) con ñ (eje paralelo a m).

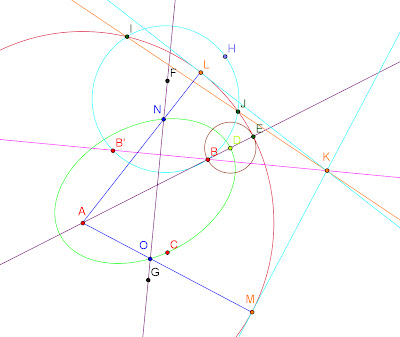
Ejercicio anterior a color Mannheim Este es un Applet de Java creado con GeoGebra desde www.geogebra.org – Java no parece estar instalado Java en el equipo. Se aconseja dirigirse a www.java.com Dada una elipse construimos dos diámetros conjugados ML IJ y por el centro K de la misma hacemos una recta perpendicular KN a uno de los diámetros IJ. Dibujamos una circunferencia cuyo diámetro sea IJ y tenemos que corta a la perpendicular anterior en el punto N que unido con el extremo del otro diámetro L tenemos una recta que la consideramos como el diámetro de la circunferencia de centro O. Uniendo este centro de la circunferencia con el centro de la elipse tenemos una recta que corta a la circunferencia azul en los puntos PQ. QL y PL son las direcciones del eje mayor y menor de la elipse, respectivamente. La distancia QK es la que corresponde al semieje menor mientras que la distancia KP es la que corresponde al semieje mayor. Ejes elípticos de Chasles Este es un Applet de Java creado con GeoGebra desde www.geogebra.org – Java no parece estar instalado Java en el equipo. Se aconseja dirigirse a www.java.com Dada una elipse definida por cinco puntos ABCDE, se trata de calcular el eje mayor y menor de la misma. Construimos dos rectas secantes paralelas a la cónica y tomamos los puntos medios GH de los segmentos que definen las secantes al cortar la elipse. Hacemos una recta que pasa por ambos puntos y tenemos un diámetro de la elipse que pasa por su centro, que es el punto medio K de IJ. Construimos una recta paralela a las dos secantes y tenemos el otro diámetro LM. Ambos diámetros son los conjugados de la elipse, los que corresponden a dos diámetros perpendiculares de la circunferencia en la que se podría transformar la elipse por proyección. Por J hacemos una recta perpendicular al otro diámetro conjugado LM y hacemos centro en este punto J para construir una circunferencia azul cuyo radio sea la distancia KM (JO). Esta circunferencia azul corta a la recta verde que pasa por el punto J en P, que unido al centro de la elipse K obtenemos un diámetro del que hacemos la circunferencia (en azul oscuro). Unimos J con el centro de la circunferencia azul obscura y tenemos que ésta recta la corta en los puntos NR. Uniendo el centro de la elipse K con RN tenemos la dirección de los dos ejes, el mayor y el menor, de la elipse. La distancia desde el punto R hasta J es el semieje menor de la elipse mientras que la distancia de N a J es el semieje mayor de la elipse. Ejes elípticos Este es un Applet de Java creado con GeoGebra desde www.geogebra.org – Java no parece estar instalado Java en el equipo. Se aconseja dirigirse a www.java.com Dada una elipse definida por cinco puntos ABCDE, determinar el eje mayor y menor, sin métodos complicados como los de Chasles y Mannheim. Según el método de Néstor Martín, modestias aparte, hacemos dos rectas secantes BF CE a la elipse, ambas paralelas, y tomamos sus puntos medios GH por los que trazamos una recta, de esta forma obtenemos la línea IJ de la que tomamos el punto medio K que es el centro de la elipse. Por el centro de la K elipse hacemos una recta paralela a la recta CE. Esta línea que acabamos de hacer y la línea IJ son los ejes conjugados de la elipse. Hacemos una circunferencia verde cualquiera tomando como centro el de la elipse y un radio menor que el eje mayor del elipse. Esta circunferencia verde corta a la elipse en MN. Los unimos mediante una recta y hacemos su mediatriz determinando en la intersección con la elipse el punto O. El segmento OK es el semidiámetro mayor de la elipse mientras que una perpendicular a este segmento por el centro de la elipse nos determina una línea que corta a la elipse en el punto P. El segmento PK es el otro semidiámetro del elipse, el menor. Teorema de Dandelin Existen 1 o 2 esferas tangentes interiores a un cono y a un plano de sección. Este plano determina los focos de las cónicas en los puntos de tangencia con las esferas. Los planos que definen la intersección de las esferas con el cono (2 circunferencias) y el plano de la cónica determina las directrices de la misma. En este perfil observamos 2 esferas (en rosa y amarillo) con un plano p tangente a ambas. Este plano p que secciona al cono según la elipse azul m de eje mayor TY (extremos de la sección del cono). La intersección de p y los planos donde las esferas son tangentes al cono: j, k, son 2 rectas paralelas al eje menor. El plano p lo proyectamos y abatimos para obtener en verdadera forma la elipse. El eje mayor TY de la elipse se transforma al proyectarla en T’Y’, el centro de la elipse es el punto medio O’ por ser una curva simétrica respecto a los dos ejes principales. Los focos son los puntos de tangencia DF de las esferas con el plano p proyectados sobre la elipse: D’F’. Para obtener el semieje menor de la elipse LO se hace un plano e por O perpendicular al eje del cono en cuya sección abatida lo observamos en verdadera magnitud. A continuación lo colocamos sobre la elipse azul ortogonal a T’Y’ y a partir del centro de la elipse: L’O’. ------------------------------------------------------------------------------------- Tangentes desde N (intersección de la directriz y prolongación del eje mayor de la elipse) a la c. focal y a la elipse. En la figura podemos observar  el alzado de un cono con dos esferas interiores tangentes al mismo. Un plano oblicuo que secciona al cono y que es tangente a las dos esferas en dos puntos, intercepta como sección una elipse cuyos focos son los puntos de contacto con las esferas, conforme al teorema de Dandelin. Este plano que vemos en el perfil, proyectante vertical llamado en el dibujo e, intercepta con el contorno del cono en los vértices de la elipse JK. El punto medio L entre estos dos vértices es el centro de la elipse. Hemos hecho la sección abatida, que significa que hemos cogido la elipse de color azul y la hemos girado 90° respecto a su eje mayor hasta hacerla coincidir en verdadera forma con el alzado de la figura. Al hacer una recta perpendicular  al eje mayor de la elipse desde uno de los focos F obtenemos el punto M en la intersección con la elipse. Al hacer una recta tangente -en color azul- por M obtenemos en la intersección con el eje mayor el punto N, por el que trazamos una recta perpendicular al eje mayor, esta recta es la directriz1 de la elipse. También la podemos obtener como intersección de los dos planos, el plano de corte e correspondiente a la elipse,  con la prolongación del plano de contacto correspondiente a la circunferencia de intersección de la esfera inferior con el cono, esto es, el plano que pasa por E-F1. Si construimos la circunferencia focal, podemos observar que el punto de tangencia F'2 de la recta tangente que pasa por N hasta la circunferencia focal, es  el punto simétrico  del foco F respecto al eje correspondiente a  la recta tangente azul anterior tg, la recta tangente a la elipse. ----------------------------------------------- En el dibujo tenemos un ejercicio como el anterior, un cono en el alzado seccionado por un plano que al mismo tiempo es tangente a dos esferas. En el alzado los elementos se transforman en dos rectas correspondientes al contorno y al mismo tiempo generatrices del cono que se cortan en C, o vértice del cono, el plano de sección en la recta HI y las dos esferas en circunferencias ocre y morada. Si construimos la circunferencia principal cuyo diámetro es la longitud del segmento en alzado con los extremos de corte del cono, esto es, los puntos HI y tomando como centro el punto medio J de estos dos extremos hacemos la circunferencia de radio JM, siendo M la intersección de la recta perpendicular al eje mayor HI por el centro J (punto medio) con la circunferencia principal de radio JH. Si trasladamos el centro J de esta circunferencia principal hasta uno de los focos  de la elipse, por ejemplo el punto G, que es el punto de contacto del plano de sección con una de las esferas, obtenemos la circunferencia verde de centro G y radio GN. Esta circunferencia corta al eje JM en el punto amarillo O, que es el vértice de la elipse correspondiente a uno de los extremos del eje menor de la elipse. Esto se basa en que el semieje mayor JH es igual  a OG. ----------------------------------------------------------------------------- Tangentes a las cónicas. Para hacer las tangentes t1 t2 a una cónica cualquiera desde un punto P, se trazan dos secantes s1 s2 a la misma y en los cuatro puntos de intersección con la cónica se hacen las diagonales n, m y las secantes d, a. La intersección de nm y da son dos puntos por donde pasa la polar. La polar corta a la cónica en los puntos de tangencia desde donde podemos trazar las tangentes t1 t2 desde P. Con la construcción de una cadena de Steiner se puede construir una cónica: http://inversas-de-figuras.blogspot.com.es/2012/02/circunferencia.html http://tangentes-a-la-parabola.blogspot.com/ http://tangentes-a-la-hiperbola.blogspot.com/ http://tangentes-a-la-elipse.blogspot.com/ http://polaridad-involucion.blogspot.com/ http://secantes-a-conicas.blogspot.com.es/ Polo C y polar (recta verde). This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com Intersección de una recta con la elipse Para calcular la intersección de una recta FG con una elipse, se construye la circunferencia focal (circunferencia de centro en uno de los focos A y con el radio el eje mayor de la elipse AE) y a continuación se hace el punto simétrico B’ del otro foco B. A continuación construimos el centro radical K de las circunferencias que pasan por los puntos BB’ y son tangentes a la circunferencia focal. Para ello construimos una circunferencia cualquiera (en color azul) que corta a la circunferencia focal en los puntos IJ, la prolongación de la recta que define estos puntos corta a la recta que pasa por BB’ en el centro radical K, punto desde el que hacemos las tangentes a la circunferencia focal. Uniendo los puntos de tangencia LM de estas dos últimas líneas tangentes a la circunferencia focal con el foco A obtenemos en la intersección con la elipse los dos puntos de corte NO de la recta dada con la elipse. ------------------------------------------------------------------------------------------------- Transformar elipse y circunferencia en circunferencia en elipse, respectivamente, de manera que las elipses sean proporcionales Tenemos en planta una elipse de color gris y una circunferencia de color verde, se trata de considerar el plano horizontal que las contiene y empezar a girarlo hasta que la elipse se convierta en una circunferencia y la circunferencia se convierta en una elipse semejante a la anterior, esto es, que tenga la misma relación entre ejes. Cogemos en la proyección vertical un plano de canto o proyectante vertical y lo empezamos a girar trasladando la distancia del eje mayor de la elipse gris hasta que corte a la línea horizontal de tamaño cuatro, que es en realidad el eje menor de la elipse. En el momento en que esta horizontal de tamaño cuatro intercepte al giro del eje mayor, habremos obtenido la posición exacta del ángulo del plano de canto que transforma a la elipse de color gris en la circunferencia de color rosa. Necesariamente ese plano de canto contiene también a la nueva elipse proporcional a la anterior y que es la figura transformada de la circunferencia verde, ya que es si el eje mayor de la elipse gris se transforma en la medida del eje menor de la elipse tornándose circunferencia, necesariamente, el diámetro de la circunferencia verde se transformará por analogía en el diámetro menor de la elipse verde, ya que existe una proporcionalidad en la que la elipse de color gris es a la circunferencia rosa como la circunferencia verde es nuevamente a la elipse azul de menor tamaño. ------------------------------------------------------------------------------------------------------------------------ Tangentes de la elipse, construcción considerando la circunferencia focal. Ejercicios construidos mediante propiedades de la circunferencia focal. La circunferencia focal (en color rosa) es aquella que podemos construir tomando centro en uno de los focos F1 y radio igual al eje mayor de la elipse AC. Existe una peculiaridad importante de esta circunferencia y es que si hacemos una recta tangente a, a la elipse, al hacer el simétrico H de uno de los focos F2 respecto a esta recta tangente obtenemos un punto que pasa por la circunferencia focal, además, si unimos este punto con el otro foco obtenemos en la intersección con la recta tangente el punto de tangencia M de esa recta tangente con la elipse. Esta característica nos sirve para hacer numerosos ejercicios. Dados los dos focos de una elipse F1 F2 y una recta tangente a, determinar los ejes mayor y menor de la elipse. Construimos el punto simétrico  del foco segundo F2 respecto a la recta tangente, de esta manera obtenemos el punto H. Unimos este punto con el otro foco F1, donde esta recta azul corta a la tangente dada obtenemos el punto de tangencia M. Si tenemos este punto que corresponde a la elipse ya tenemos los demás datos, ya que sabemos que la distancia de H a un foco sumado a la distancia de ese mismo punto al otro foco es igual al eje mayor de la elipse, por tanto tomamos estas dos distancias sumadas y las convertimos en un solo segmento y lo centramos en la línea que pasa por los focos de la elipse, pudiendo dibujar así el eje mayor de la misma  AC. Por el punto medio de este segmento –el origen de coordenadas- hacemos una recta perpendicular al eje mayor, y tomando la distancia desde el centro de la elipse hasta uno de los vértices, por ejemplo el punto C, hacemos centro en uno de los focos, y construimos un arco que corta a la perpendicular anterior en dos puntos, los correspondientes a los vértices de los ejes menores de la elipse, los puntos BV. Este último trazado se basa en que la distancia desde el vértice  B hasta el foco F2 es igual a la distancia desde el centro de la elipse al vértice C. Dados dos focos de una elipse y un punto H de su circunferencia focal, determinar los ejes mayor y menor de la elipse. Unimos el punto de la circunferencia focal dado H con el foco más cercano F2, por el punto medio de este segmento trazamos la perpendicular o mediatriz, esta recta será tangente a la elipse. Para calcular el punto de tangencia con la elipse unimos el punto dado de la circunferencia focal con el otro foco, donde esta recta H-F1 corte a la tangente a obtenemos el punto de tangencia M. A partir de aquí ya es igual al ejercicio anterior. Dada la circunferencia focal –en color rosa- y uno de los focos de la elipse –el que no es centro de la circunferencia focal, o sea F2-, determinar puntos de la elipse. Tomamos un punto cualquiera de la circunferencia focal, por ejemplo el punto H, lo unimos con el foco dado F2 mediante un segmento del que calculamos la mediatriz a. Uniendo el punto H con el centro de la circunferencia focal F1, que se obtiene por la intersección de dos mediatrices de dos rectas secantes cualesquiera de la circunferencia, obtenemos en el punto de intersección de este segmento F1-H con la recta tangente a, un punto de la elipse M, que al mismo tiempo es el punto de tangencia de la recta tangente a la elipse. Para calcular otros puntos se hace exactamente igual, se toma un punto cualquiera de la circunferencia focal y se une con el foco dado, la mediatriz es otra tangente a la elipse de la que calculamos el nuevo punto como intersección del segmento que une el centro de la circunferencia focal con el nuevo punto escogido de la circunferencia focal. Dada la circunferencia focal y una recta a tangente a la elipse además del punto de tangencia M, determinar los ejes mayor y menor de la elipse. Calculamos el centro de la circunferencia focal, que será uno de los focos de la elipse. Para construirlo dibujamos dos rectas secantes cualesquiera de la circunferencia focal, construimos sus mediatrices y en el punto de intersección de ambas obtenemos el centro de la misma. Unimos el centro de la circunferencia focal F1 con el punto de tangencia M y prolongamos esta recta hasta que corte a la circunferencia focal en el punto H. Calculamos el simétrico de H respecto a la recta tangente dada, este nuevo punto obtenido es el otro foco de la elipse F2. Como ya tenemos los focos y un punto de la elipse M podemos obtener los demás datos. ------------------------------------------ Dadas dos rectas tangentes a la elipse (a,b) y la circunferencia focal, obtener los ejes mayor y menor de la elipse. Como el foco F2 es un punto simétrico respecto a un punto H de la circunferencia focal, siendo el eje de simetría la recta tangente, tomamos el segmento circular de la recta tangente a, la franja correspondiente al tono amarillo superior, y hacemos lo mismo con el segmento circular de la recta b. Al hacer las figuras simétricas de los segmentos circulares amarillos anteriores obtenemos las formas geométricas en azul y verde claro, la intersección de las circunferencias de ambos segmentos circulares determinan el foco F2. Si tenemos los dos focos y las rectas tangentes podemos obtener ya los demás elementos de la elipse, ya que desde el foco hacemos las rectas perpendiculares a ambas tangentes y obtenemos como simétrico de éste punto respecto a las rectas tangentes dos puntos H I de las circunferencias focales que unidos con el otro foco F1 determinan en la intersección con las tangentes los puntos de tangencia MG. -------------------------------------- La circunferencia principal respecto a las tangentes de la elipse Para toda tangente de la elipse, en el dibujo en color verde, se tiene que es la bisectriz de dos rectas que pasan por los focos y por un punto de la misma (bisectriz de las rectas AF y BF).  Como podemos observar en el dibujo al prolongar la recta obtenemos en la intersección con la circunferencia focal CF (circunferencial cuyo centro está en uno de los pocos del elipse y radio el eje mayor del elipse), el punto simétrico del foco B respecto a la tangente.  Como podemos observar también en el dibujo el punto de intersección de la recta amarilla que une los dos puntos simétricos BB' con la tangente es siempre un punto G de la circunferencia principal, circunferencia de color azul en el dibujo que pasa por los vértices TC del eje mayor de la elipse y cuyo centro R es también el de la elipse. ---------------------------------------------------- En la figura podemos observar una elipse en un alzado que se ha girado 90 grados para ver la posición exacta de los focos AB y los vértices CD, en esa elipse se apoya en uno de sus focos B una esfera c en color ocre, como podemos observar en los dos dibujos la esfera cambia de tamaño y un cono tangente a la misma del que vemos el contorno FG en el dibujo, tenemos que el vértice H de ese cono nos define siempre puntos una hipérbola- en color verde en el dibujo. En la figura podemos observar una elipse con el eje mayor CD y sus dos focos AB, sobre uno de sus focos B representamos en el alzado una esfera que tiene por proyección la circunferencia ocre amarilla c, al variar esta esfera y darle un tamaño mayor siempre apoyándose en el foco B  de la elipse podemos observar que todos los conos tangentes a la esfera y que tienen por proyección en alzado como contorno en las generatrices los vértices de la elipse CD,  pues  los vértices H de esos conos determinan  una hipérbola - en el dibujo de color verde.   La proyección de la elipse en un alzado,  junto con la proyección de la esfera que se apoya siempre en el foco  y la proyección del contorno del cono en el que se ven las generatrices tangentes FG a la esfera,  se puede comprobar que ambas tangente se cortan en un punto H  que siempre es un vértice de la hipérbola.   En el momento en que las tangentes fueran paralelas tendríamos que el cono se convertiría en cilindro y obtendríamos el punto del infinito de la hipérbola que es el punto del infinito de las asíntotas. En la figura podemos observar una elipse,  se trata de hacer una figura desde la que desde todos los puntos la podamos observar bajo un ángulo de 90 grados,  esto quiere decir que al verla bajo ese punto de vista siempre acotamos sus extremos bajo dos líneas que forman entre sí 90 grados. Para realizar esa figura dibujamos por los vértices C y E  dos líneas paralelas a los ejes principales, - en el dibujo en color siena y morado-,  la intersección de estas dos paralelas determinan el punto H. La circunferencia azul de radio DH  es la solución,   desde cualquier punto que cojamos de esta circunferencia,  hacemos las dos tangentes a la elipse y podemos observar que siempre formarán entre sí  90 grados.  Tenemos por ejemplo el punto rojo I  desde el que hacemos las dos tangentes negras a la elipse y vemos que forman el ángulo verde de 90 grados,  esa condición la cumplen todos los puntos de la circunferencia. --------------------------------------------- Tenemos un punto exterior O a la elipse desde el que queremos hacer   las tangentes a la elipse  Hacemos una circunferencia que tenga por  centro ese punto y por radio la distancia hasta el foco B De esta manera tenemos una circunferencia verde que corta a la distancia focal k en  en 2 puntos,  si esos puntos los unimos con el foco obtendremos dos segmentos cuyas mediatrices son las tangentes desde el punto dado.  La elipse es el lugar geométrico de  los centros cuyas circunferencias son tangentes a la circunferencia focal k, circunferencia que se obtiene haciendo centro en un foco y con  el radio  correspondiente al eje mayor de la elipse   --------------------------------------------- Tenemos una elipse C en color violeta y queremos calcular su centro H y ejes principales m n- en color verde- trazamos dos cuerdas DE, FG y tomamos sus puntos medios H I por los que trazamos una recta h, esta recta corta a la elipse en dos puntos JK, tomamos el punto medio H de esos dos y ya tenemos el centro de la elipse.  Tomamos el centro H y hacemos una circunferencia que corte a la elipse, lo hace según cuatro puntos RSPQ que determinan un rectángulo negro y cuyos lados son la dirección de los ejes, direcciones que trazamos por el centro de la elipse, con lo cual ya tenemos los dos ejes principales de la elipse, el mayor y el menor, ambos en color verde. ---------------------------------------------- En la figura tenemos una elipse y un punto exterior P desde el que vamos a trazar las tangentes rojas f g; para ello hacemos una circunferencia cuyo centro P sea el punto dado y que tenga por radio la distancia PF'. La intersección de esa circunferencia con la circunferencia focal e' realizada con el centro en el otro foco F y por radio la distancia 2a, o sea el eje mayor, nos da como intersección B' y B'1 que son los simétricos del foco primero respecto a las tangentes.  Si unimos cada uno de esos 2 puntos con el foco F' y trazamos las mediatrices por esas dos líneas secantes a la cónica tendremos que son las tangentes f g  que pasan por el punto dado P. Si los puntos de intersección B' y B'1 los unimos con el otro foco F obtenemos en la intersección con la cónica H E que serán los puntos de tangencia.  Como podemos observar los triángulos verdes definen en sus lados dos perpendiculares que pasan por el punto dado P y son perpendiculares a los lados de los triángulos mientras que el vértice opuesto H E de cada triángulo corresponde a los puntos de tangencia; lo mismo pasa con los triángulos azules,  sus vértices son los puntos de tangencia y los lados opuestos a esos vértices son en realidad perpendiculares a las tangentes rojas.  Como podemos observar en los triángulos azules 3 puntos de dos de sus lados pasan por la circunferencia que tiene por centro el punto dado P y por radio la distancia desde el punto hasta ese foco F. Lo mismo pasa con la otra circunferencia que pasará por otros dos tres vértices de los triángulos verdes y que tendrá por radio la distancia desde el punto hasta el foco más cercano F'. Si nos fijamos las tangentes son las bisectrices del eje focal de la elipse y las líneas que pasan por los puntos A1'-B1. De la misma forma estas bisectrices que son tangentes a la cónica cortan al eje focal en el mismo punto por donde pasa la simétrica del eje focal respecto a las tangentes, eso quiere decir que los puntos W Ñ están siempre sobre el eje focal. ------------------------------------------------------------------------------------------------------------------------------ Aplicaciones prácticas de las curvas cónicas y su existencia en la naturaleza. La parábola se da en los faros de los coches, en los focos, en las antenas de radio y televisión, en los radiotelescopios; todos ellos se sirven de la parábola cuyos rayos de proyección salen o entran paralelos al eje de la parábola desde o en dirección al foco. Se da también en los arcos de los puentes, en el diseño de las cabezas de misiles, en cables de puentes colgantes con carga de distribución uniforme, en estufas eléctricas, en telescopios reflectantes, en un fluido de un recipiente rotatorio por efecto de la fuerza centrífuga, excepcionalmente en órbitas planetarias bisagras entre elipses e hipérbolas -entre lento y rápido desplazamiento, respectivamente-, en superficies de carrocerías y fuselajes por su carácter aerodinámico, en la trayectoria de la curva que describe un objeto al ser lanzado con campo gravitatorio homogéneo y despreciando la resistencia al aire, como por ejemplo un misil. La parábola no hay que equivocarla con la curva catenaria, de forma parecida, que es la curva que adopta una cuerda colgada desde dos de sus puntos por su peso. Cuando varios proyectiles se disparan desde un cañón en distintas direcciones, el conjunto de las trayectorias que siguen estos proyectiles definen una envolvente que nunca es rebasada por ninguna de las trayectorias. Esta envolvente es una parábola de revolución llamada de seguridad, (esto es la superficie generada por la revolución de una semiparábola). Esta envolvente de todas las parábolas tiene en su tangente por el vértice una línea que es directriz de todas las parábolas, esto es, una recta perpendicular a todos los ejes de las parábolas. La elipse se da en las órbitas de los cuerpos celestes que giran en torno a otro, en misiles con trayectoria intercontinental en los cuales hay mayor fuerza y donde g ya no es constante. La elipse se da en secciones de bóvedas y formas de distintos arcos, también en la perspectiva de nuestra percepción las circunferencias las podemos ver como elipses. La bóveda del techo del andén del metro tiene una curvatura elíptica, lo que facilita una buena acústica. Las piedras erosionadas por el agua del río son formas aproximadas a elipsoides cuyas secciones se acercan en la forma a secciones elípticas. La perspectiva oblicua de una circunferencia desde una proyección paralela o cilíndrica sobre un plano es una elipse (siempre y cuando los planos no sean paralelos), si la proyección es cónica resulta una cónica cualquiera. Si 2 jugadores nos pasamos el balón dentro de un recinto sin necesidad de tener que coger nunca la pelota, debemos disponer de un recinto con forma elíptica. Nos colocamos en los focos de la elipse y cuando el balón rebote con los muros en forma de elipse siempre irá a la otra posición donde está la otra persona, en el otro foco de la elipse. Si juego yo solo al frontón contra las paredes y quiero que el balón siempre venga de vuelta, la elipse debe tener sus 2 diámetros iguales, esto es, ser una circunferencia. La hipérbola se da en el redondeo de piezas, en la proyección de las sombras de casi todos los focos y pantallas que hay en la casa, en la intersección de las circunferencias equidistantes que provocan dos piedras lanzadas al agua, en las centrales térmicas de torres de refrigeración. La hipérbola es la curva fronteriza o envolvente de una zona de audio: un avión que se desplaza con velocidad constante y movimiento rectilíneo propaga el ruido de su motor en esferas crecientes. Según se desplaza las esferas que va dejando atrás son cada vez mayores y la curva envolvente de esas esferas es un hiperboloide. La proyección ortogonal de estas esferas y del hiperboloide es, respectivamente, un conjunto de círculos y una hipérbola envolvente a las mismas. Cuando un palo está clavado ortogonalmente sobre el suelo y es iluminado por el sol, la sombra que produce el extremo del palo es una hipérbola. Las curvas cónicas se dan en general en casi todos los diseños en los que se quiere que las superficies sean suaves y aerodinámicas, esto es, que no se note la transición entre en el enlace de las superficies, como son las superficies de cascos de barcos, de fuselajes de aviones, de carrocerías de automóviles, etcétera. http://la-aerodinamica.blogspot.com/ También se dan de forma genérica en los movimientos de cuerpos celestes, que según la fuerza de atracción puede generar cualquiera de las cónicas: si el objeto sigue una trayectoria rectilínea por el espacio -despreciando la curvatura del espacio- y es atraído por la órbita de otro describe una forma hiperbólica, excepcionalmente parabólica. Si el objeto que lo atrae tiene fuerza suficiente para incorporarlo en su propia órbita, éste describe una curva elíptica en cuyo foco está el objeto. Las bóvedas tienen por sección formas cónicas y los arcos suelen tener por lo general forma parabólica, elíptica o circular. Igual que en las leyes de la mecánica, que provocan que la trayectoria del balón salga de un foco de la elipse y choque con una pared del campo elíptico y vaya al otro foco, pasa lo mismo con las leyes de la reflexión y refracción en óptica con todas las cónicas. Un rayo de luz que salga de un foco rebota en la pared de un espejo elíptico y vuelve al otro foco. En el caso de la parábola si el punto de luz está en el foco de la misma, el rayo, al tocar la superficie parabólica, sale reflejado en una dirección paralela al eje de revolución del paraboloide por eso todos los faros son paraboloides de revolución, mientras que si la superficie es hiperbólica, el rayo de luz que sale del foco rebota con la superficie y sigue una dirección definida por ese punto y el otro foco.